

Pourriez-vous trouver un
nombre qui donne un résultat autre que 9?
A part si on garde le même
nombre, ce qui donnera 0, on obtiendra toujours 9.
La démonstration
est mathématique. J'essaierai de trouver plus tard une explication
simple.
Prenons un nombre n de 4
chiffres comme exemple, soit abcd (si n est 1975, a=1, b=9,…).
On a donc n=a*1000+b*100+c*10+d.
Appelons m le nombre n avec
les chiffres dans n'importe quel ordre. On veut montrer que n-m est dividible
par 9, soit que la somme de ses chiffres est égale à 9.
On va donc calculer n modulo
9: n[9].
n[9]=a[9]*1000[9]+b[9]*100+c[9]*10[9]+d[9].
Or, et c'est là toute
l'astuce, 10 puissance p modulo 9 est toujours égal à 1.
C'est pour cela que si l'on additionne les chiffres d'un multiple de 9,
le résultat est 9.
Donc, n[9]=a[9]+b[9]+c[9]+d[9].
De même, m[9]= a[9]+b[9]+c[9]+d[9].
Donc, (n-m)[9]=0… Le nombre
est divisible par 9.
Comment se présentait
l'échiquier que les blancs ne jouent?
La tour blanche était
un pion situé entre le fou blanc et le roi…
Le roi noir est en échec
par le fou et la tour en même temps. Le seul moyen d'obtenir cela,
c'est qu'au tour précédent, soit le fou est entre le roi
et la tour (ce qui est impossible), soit que la tour soit entre le fou
et le roi, ce qui n'est possible que si la tour a pu faire le déplacement
dans le coin.
La tour était donc
un poin entre le roi noir et le fou blanc. Ce poin a mangé une pièce
noire dans le coin et s'est transformé en tour!
Rébus:
Un grand AB plein d'"a"
petits "a" traversé par "i" 100 sous p.
Un grand abbé plein
d'appétit a traversé Paris sans souper.
Comment faire 6 triangles
équilatéraux avec 6 allumettes?
En dessinant une étoile
de David.
Comment faire 4 triangles
équilatéraux avec 6 allumettes?
En faisant une pyramide
(3 dimensions).
Comment passer par tous les points en 4 droites et sans lever le crayon?

Comment faire quatre droites
perpendiculaires ayant chacune une valeur de 1,5 francs?
Dessinez un carré
sur une feuille et placez 1,5 Francs à chaque coin!
Quelle est ligne suivante
de cette suite logique?
13112221.
La ligne précédente
était 312211.
Il suffit de lire la ligne:
D'abord, il y a un 3 (13), puis un 1 (11) puis deux 2 (22), puis deux 1
(21).
La ligne qui suivra 13112221
sera 1113213211.
Essayez maintenant de démontrer
qu'il n'y aura jamais de 4…
Pourriez-vous la réparer
en ouvrant uniquement trois anneaux?
On a cinq morceau de 3 anneaux.
Il faut ouvrir les 3 anneaux
d'un même morceau pour y arriver.
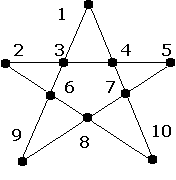
Pouvez-vous placer 9 des
10 points et expliquer la méthode pour y parvenir?
Un ordre de placement possible
est 4, 2, 8, 5, 3, 9, 7, 1, 6.
Le principe est de mettre
un point au départ et de placer le point que l'on ne pourra plus
placer par celui qu'on vient de mettre.
En clair, on place le point
4 (par exemple). On ne pourra plus placer le point 2 par le point 4. On
place donc le point 2 (par le point 8). En plaçant le point 2, on
ne pourra plus placer le point 8 par le point 2. On place donc le point
8 par le point 5, et ainsi de suite…
Comment se fait-il qu'on
le trouve toujours au dernier endroit où l'on a regardé?
Si on a trouvé, pourquoi
regarderait-on ailleurs? C'est donc toujours au dernier endroit où
l'on regarde qu'il y a ce que l'on cherche…